数学奖章上的数学故事

源济

菲尔兹奖 | 数学奖章上的数学故事（连载一） 

2016-04-29 欧阳顺湘 好玩的数学

有许多用著名数学家的名字来命名的数学奖，如费马奖、康托奖和欧拉奖等等。其中许多是“单项奖”，奖励在某些方面（往往是用来命名的数学家有所建树的领域）成就卓著的数学家。如欧拉奖（Euler Prize）自1993 起在每年的国际组合数学年会上颁发给在组合数学领域有突出贡献的数学家。也有不少“终身成就奖”，著名的有2001 年设立的阿贝尔奖。该奖由挪威王室一年一度颁给杰出数学家，奖金达80 万美元，媲美诺贝尔奖奖金，是世界上奖金最高的数学奖。

本系列文章选自于《数学文化》第二卷第4期，我们将从国际数学家大会四大奖项和国际数学教育大会两大奖项，欣赏奖章，了解相关的数学家和数学知识。

菲尔兹（John Charles Fields,1863-1932 年）

菲尔兹奖由加拿大数学家约翰• 查尔斯• 菲尔兹（John Charles Fields,1863-1932 年）建议设立。菲尔兹早年游学美国、欧洲，与诸多大数学家共事。其后返回加拿大致力于提升数学的地位。如在他努力下，1924 年世界数学家大会在加举行。他自上个世纪20 年代末开始筹备该奖，并遗嘱捐赠$47,000给奖项基金。菲奖在1936 年首颁；后从1950 年起每隔4 年颁发一次，奖励40 岁以下数学成就杰出者，且旨在鼓励获奖者进一步的研究。获奖者一般为2 至4 人。该奖有“数学界中诺贝尔奖”之称，其实它早期并无今日如此声誉，这很大程度上源于历届获奖者给它带来的荣耀。

菲尔兹奖包括一面金质奖章和一笔不算多的奖金（目前为15,000 加元）。奖章正面有古希腊数学家阿基米德的头像（Archimedes, 前287- 前212 年）和希腊文“ΑΡΧΙΜΗΔΟΥΣ”，意为“阿基米德的（头像）”；头像周边刻拉丁文“TRANSIRE SUUM PECTUS MUNDOQUE POTIRI”，此来源于一世纪罗马诗人马尼利乌斯（Manilius）的著作《天文学》，意为“超越他的心灵，掌握世界”。此外奖章设计者（Robert Tait McKenzie）名字之缩写RTM 及设计年份MCNXXXIII（即1933 年，第二个M 字母以N 代）也刻在奖章上。获奖者的名字则会被刻于奖章边轮。

菲奖章背面刻有意为“聚全球数学家，为杰出著作而颁”的拉丁文“CONGREGATI EX TOTO ORBE MATHEMATICI OB SCRIPTA INSIGNIA TRIBUERE”。文字和树枝的背景为球体嵌进圆柱体（“圆柱容球”）的示意图，这象征着阿基米德的得意之作《论球与圆柱》中最著名的一个结果：球与其外切柱体的面积（体积）之比为2 : 3。阿基米德对此如此骄傲，以致他希望人们在他的墓碑上刻下球与圆柱体的关系图。确实，阿基米德计算各种面积所用的“穷竭法”可以被视作后世微积分学所用“无穷小分析”的起源。

球与其外切柱体的面积（体积）之比为2 : 3 ：若设球半径为r，则球面积为4πr²，体积4/3πr3 ；而其外切柱体面积为6πr²，体积为2πr3

传说正沉思于几何问题的阿基米德被鲁莽无知的罗马士兵杀死之后，罗马将军马塞勒斯悲伤不已，不但给阿基米德立墓，备极哀荣，并按他生前的愿望在碑上刻球内切于圆柱的图形。在公元前73 年，时任西西里岛财务官的罗马著名政治家、哲学家西塞罗（Marcus Tullius Cicero, 前106- 前43 年）去叙拉古（Syracuse）探访阿基米德之墓。其时阿基米德去世才137 年，当地人却已对阿基米德之墓一无所知，否认有这样一个墓。通过一番搜索，西塞罗终在杂草丛中凭此球内切圆柱图案辨认出阿基米德的墓，并派人去清理繁芜，铺砌道路。西塞罗在他的文章中写道，找到阿基米德之墓后，他告诉叙拉古人，此刻他和叙拉古最杰出的人在一起，而这正是他一直在寻求的。后来一些画家还将此刻情景凝固在油画中。其中著名的有美国画家本杰明•威斯特（Benjamin West, 1738-1820）1797 所作的油画“西塞罗发现阿基米德之墓”（1804 年他另作一幅稍有差别的画）。两个名人穿时空的重逢确是值得纪念的。这种对文明的尊重弥足珍贵的另一个原因是对数学家的尊重在西塞罗那个时代是少见的。西塞罗曾写道“几何学在希腊人中享有极高声誉，没有什么比数学更加荣光的了；但我们（罗马人）却只满足于那些用来计算和测量的数学知识”。

今日意大利西西里岛阿基米德家乡叙拉古的“阿基米德的坟墓”遗址

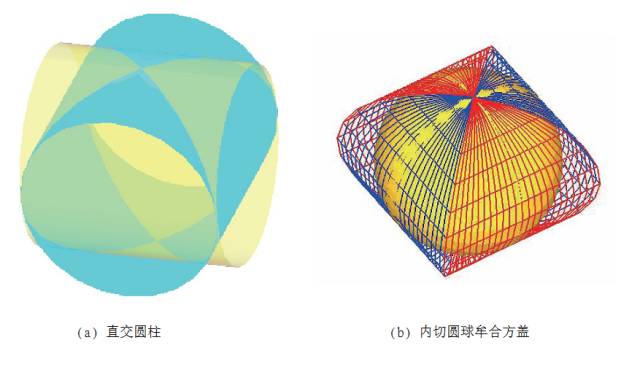
类似于阿基米德的“穷竭法”和圆柱容球的比例2 : 3，我国三国时代魏国数学家刘徽也应用类似的极限思想求出了圆面积、一些锥体（如阳马与鳖臑）的体积。而且他还在评注我国算术名著《九章算术》时正确地猜测了球体积与其外切牟合方盖体积之比等于圆与其外接正方形的面积之比（即π :4）。这里所谓的“牟合方盖”是一个立方体从纵横两个方向做内切圆柱的共同部分，因其外型酷似上下相对（牟合）的方伞（盖）。中国家庭日常生活中常用的食物罩就类似牟合方盖的一半。

原来在《九章算术》的“少广”章中记有“开立圆术”，认为直径为D的球体积公式为

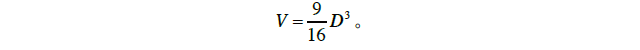
如果将π 取值为3，则该公式相当于认为球体积与其外切圆柱体积之比为3:4。刘徽指出这是错误的，但他自己没能求出牟合方盖的体积从而得出正确的球体积计算公式，而是将这个问题留给了后人，“以俟能言者”。

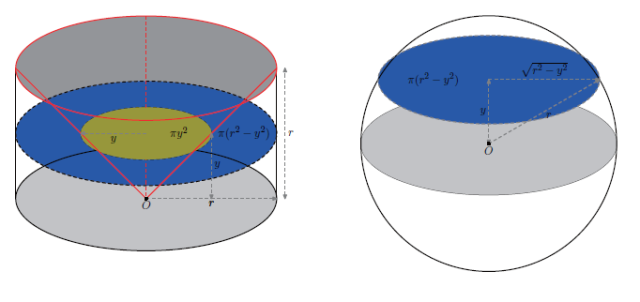
半球体积与圆柱体去掉锥体剩余部分体积相同（横截面（图中蓝色部分）面积相同）

刘徽去世之后200 余年，南北朝时期的祖冲之、祖暅父子共同提出了祖暅原理：所有等高处横截面积相等的两个同高立体，其体积也必然相等（“缘幂势既同，则积不容异”）。该原理在西方常被称为卡瓦列里原理，因由意大利几何学家卡瓦列里（Bonaventura Francesco Cavalieri, 1598 年-1647 年）重新发现。这可以看作是微积分学发展历程中自阿基米德的穷竭法之后的一大进步。祖氏父子正是利用此原理算出牟合方盖的体积从而得出球体体积。

刘徽提出的球体体积与牟合方盖的体积之比则是祖暅原理的直接推论：因为我们可将球体当作由横截的圆累积而成；若将这些横截圆改为外接该圆的正方形，则所得立体即是牟合方盖。我们这里仅简单介绍如何用祖暅原理来理解阿基米德提出的比例。

在底面半径和高均为r 的圆柱体中倒立一个以圆柱体上表面为底，下底面圆心为顶点的圆锥。易由勾股定理得知半径为r 的半球“赤道”上方y处横截面（半径为 √（r²—y^2） 的圆）的面积为π(r² － y²) ；而等高处圆柱体的横截面的面积（恒为πr²）去掉锥体的横截面积（πy²）为π(r² － y²)。由祖暅原理，半球体积等于圆柱体中除去圆锥体所剩部分之体积。我们知道内嵌圆锥体体积是柱体体积的三分之一，因此半球体积是三分之二倍此圆柱体体积。

"延伸阅读

国际数学家大会上四大奖项

在德国数学家联合会（Deutsche Mathematiker-Vereinigung, 简称DMV）主席康托的积极努力下，首届国际数学家大会（International Congress of Mathematicians, 缩写为ICM）于1897 年在瑞士苏黎世召开。自1900 年在巴黎召开了第二次会议后，每四年举行一次。但后因二战而停办。1950 年国际数学联盟（International Mathematical Union, 缩写为IMU）成立，国际数学家大会的传统才得以恢复。现在国际数学家大会最令人瞩目的要事之一便是开幕式上颁发的四大奖项：菲尔兹奖、奈望林纳奖、高斯奖和陈省身奖。

源济

奈望林纳奖 | 数学奖章上的数学故事（连载二） 

2016-05-01 欧阳顺湘 好玩的数学

有许多用著名数学家的名字来命名的数学奖，如费马奖、康托奖和欧拉奖等等。 其中许多是“单项奖”，奖励在某些方面（往往是用来命名的数学家有所建树的领域）成就卓著的数学家。如欧拉奖（Euler Prize）自1993 起在每年的国际组合数学年会上颁发给在组合数学领域有突出贡献的数学家。也有不少“终身成就奖”，著名的有2001 年设立的阿贝尔奖。该奖由挪威王室一年一度颁给杰出数学家，奖金达80 万美元，媲美诺贝尔奖奖金，是世界上奖金最高的数学奖。

本系列文章选自于《数学文化》第二卷第4期，我们将从国际数学家大会四大奖项和国际数学教育大会两大奖项，欣赏奖章，了解相关的数学家和数学知识。

奈望林纳奖由国际数学联盟于1981 年设立，奖励在信息科学的数学方面有突出贡献的年轻数学家。它类似于菲尔兹奖，得奖者必须在获奖那一年不大于40 岁。该奖包括一枚奖章和部分奖金，每四年在国际数学家大会颁发，且获奖者的名字也会被刻在奖章边轮。奈望林纳奖于1982 年首颁，有“计算机科学中诺贝尔奖”之称。奈望林纳奖是以纪念在1980 年去世的芬兰最著名的数学家之一罗尔夫• 奈望林纳（Rolf Herman Nevanlinna, 1895-1980 年）。奈望林纳在函数论方面贡献卓著，且在20 世纪50 年代开启了芬兰的计算机项目。

1982 年，国际数学联盟接受赫尔辛基大学对该奖的资助。奖章正面为奈望林纳的头像以及文字“ROLF NEVANLINNA PRIZE”（“奈望林纳奖”）以及很小的字符“RH 83”（示意此奖章由设计者 Raimo Heino 于1983 年首次铸造），反面的两个图案都和赫尔辛基大学有关。奈望林纳是赫尔辛基大学的教授，并曾任校长。右下角是赫尔辛基大学的校徽，环绕校徽有赫尔辛基大学的名字“UNIVERSITAS HELSINGIENSIS”。左上角是文字“Helsinki”的编码，这和该奖的表彰内容相得益彰。例如，2010 年获得奈望林纳奖的Daniel Spielman 的一个主要贡献即是关于编码理论的。